To calculate the mass of a planet, we need to know two pieces of information regarding the planet,
- Time is taken by an object to orbit the planet,
- Distance between the object and the planet.
These are the two main pieces of information scientists use to measure the mass of a planet. The time taken by an object to orbit any planet depends on that planet’s gravitational pull. So if we can measure the gravitational pull or acceleration due to the gravity of any planet, we can measure the mass of the planet.
There are other methods to calculate the mass of a planet, but this one (mentioned here) is the most accurate and preferable way. Because other methods give approximation mass values and sometimes incorrect values.
Though most of the planets have their moons that orbit the planet. With the help of the moon’s orbital period, we can determine the planet’s gravitational pull. But few planets like Mercury and Venus do not have any moons.
So… in this type of case, scientists use the spacecraft’s orbital period near the planet or any other passing by objects to determine the planet’s gravitational pull.
Here in this article, we will know how to calculate the mass of a planet with a proper explanation.
Mathematical calculation of the mass of a planet
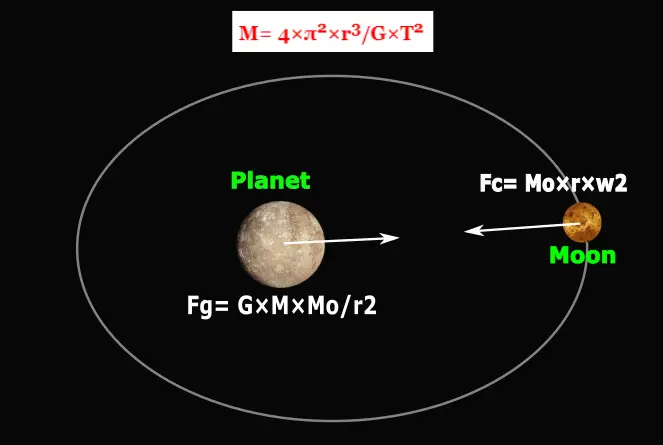
The most accurate way to measure the mass of a planet is to determine the planet’s gravitational force on its nearby objects. And those objects may be any moon (natural satellite), nearby passing spacecraft, or any other object passing near it.
Here we will consider,
- there is a planet with a mass of “M”,
- a moon orbiting the planet with a mass of “Mo” and it takes time “T” to complete one orbit around the planet,
- the distance between the moon and the planet is “r”.
Now we will calculate the mass ‘M’ of the planet.
According to Newton’s law of universal gravitation, the planet would act as a gravitational force (Fg) to its orbiting moon.
Fg= G×M×Mo/r2
- Where G is the Universal Gravitational Constant and G=6.67 × 10-11 Nm2/kg2.
To maintain the orbital path, the moon would also act centripetal force on the planet. According to Newton’s 2nd law of motion:
Centripetal force, Fc= Mo×Ac
- Where ‘Ac‘ is centripetal acceleration.
Ac= v2/r= w2×r
- Where ‘w’ is angular velocity.
And w= 2π/T
- Where ‘T’ is the orbital period of the moon around that planet. (T is known)
Fc= Mo×w2×r= Mo×r×4×π2/T2
Thus to maintain the orbital path the gravitational force acting by the planet and the centripetal force acting by the moon should be equal.
- Fg= Fc
- G×M×Mo/r2 = Mo×r×4×π2/T2
- M= 4×π2×r3/G×T2
“Hence from the above equation, we only need distance between the planet and the moon ‘r’ and the orbital period of the moon ‘T’ to calculate the mass of a planet. Because the value of ‘π’ and ‘G’ is constant and known“.
So scientists use this method to determine the planet’s mass or any other planet-like object’s mass. This method gives a precise and accurate value of the astronomical object’s mass.
How do scientists measure the planet’s mass without the moon?
Now as we knew how to measure the planet’s mass, scientists used their moons for planets like Earth, Mars, Jupiter, Saturn, Uranus, Neptune, Dwarf Planet Pluto, and objects those have moons. But planets like Mercury and Venus do not have any moons.
Space probes are one of the ways for determining the gravitational pull and hence the mass of a planet. For example, NASA’s space probes Voyager 1 and Voyager 2 were used to measuring the outer planet’s mass. Whereas, with the help of NASA’s spacecraft MESSENGER, scientists determined the mass of the planet mercury accurately.
- Must Read:- Orbit of the International Space Station (ISS)
All the planets act with gravitational pull on each other or on nearby objects. Scientists also measure one planet’s mass by determining the gravitational pull of other planets on it. They use this method of gravitational disturbance of the orbital path of small objects such as to measure the mass of the asteroids.
Sometimes the approximate mass of distant astronomical objects (Exoplanets) is determined by the object’s apparent size and shape.
What is the mass of each planet?
The mass of all planets in our solar system is given below.
- Mercury- 3.30×1023 kg
- Venus- 4.86×1024 kg
- Earth- 5.97×1024 kg
- Mars– 6.41×1023 kg
- Jupiter- 1.89×1027 kg
- Saturn– 5.68×1026 kg
- Uranus- 8.68×1025 kg
- Neptune– 1.02×1026 kg
So… the order of the planets in our solar system according to mass is Jupiter, Saturn, Neptune, Uranus, Earth, Venus, Mars, and Mercury.
- Must check:- Mass of Planets in Order from Lightest to Heaviest
Must Read Related Articles:-
- How long is a day and year on each planet
- Closest and farthest distance of each planet
- How big are the stars? Compare to Sun and Earth
- 5 Best Solar System Backpacks in 2024
- Mass of Planets in Order from Lightest to Heaviest
- Star Projector {2024}: Star Night Light Projector